Речь пойдёт про Nvidia CUDA применительно к методу Гаусса-Жордана для обращения квадратной матрицы.

Метод состоит из следующих шагов:

• составить расширенную матрицу (справа дописать единичную),
• путем элементарных преобразований привести левую часть матрицы к единичной.

В результате в правой части расширенной матрицы получим обратную матрицу.

Алгоритм на Python

from copy import deepcopy
import sys


def words():
    """
    Чтение по словам
    """
    for line in sys.stdin:
        for word in line.split():
            yield word


def new_empty(n):
    """
    Создание новой матрицы
    """
    return [x[:] for x in [[0.0] * n] * n]


def pivotize(mat_a, x):
    """
    Путем обмена строк расположить наибольшие элементы на диагонали
    """
    mat_a = deepcopy(mat_a)
    size = len(mat_a)
    row = max(range(x, size), key=lambda i: abs(mat_a[i][x]))
    if x != row:
        mat_a[x], mat_a[row] = mat_a[row], mat_a[x]
    return mat_a


def invert(mat_a):
    """
    Обращение матрицы методом Гаусса-Жордана
    """
    mat_a = deepcopy(mat_a)
    n = len(mat_a)

    # Дополнить матрицу справа единичной матрицей
    for i in range(n):
        mat_a[i] += [int(i == j) for j in range(n)]

    # Прямой ход
    for x in range(n):
        mat_a = pivotize(mat_a, x)
        for i in range(x + 1, n):
            coefficient = mat_a[i][x] / mat_a[x][x]
            for j in range(x, n * 2):
                mat_a[i][j] -= coefficient * mat_a[x][j]

    # Обратный ход
    for x in reversed(range(n)):
        for i in reversed(range(x)):
            coefficient = mat_a[i][x] / mat_a[x][x]
            for j in reversed(range(n * 2)):
                mat_a[i][j] -= coefficient * mat_a[x][j]

    # Разделить строки на ведущие элементы
    for i in range(n):
        denominator = mat_a[i][i]
        for j in range(n * 2):
            mat_a[i][j] /= denominator

    # Оставить только правую часть матрицы
    for i in range(n):
        mat_a[i] = mat_a[i][n:]

    return mat_a


def main():
    w = words()
    n = int(next(w))
    mat_a = new_empty(n)
    for i in range(n):
        for j in range(n):
            mat_a[i][j] = float(next(w))

    result = invert(mat_a)
    for i in range(n):
        for j in range(n):
            print('{:.6e}'.format(round(result[i][j], 10)), end=' ')
        print()


if __name__ == '__main__':
    main()

На C++

#include <iostream>
#include <iomanip>
#include <cmath>

using namespace std;

void print(double *matrix, int n) {
  cout << scientific;
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      cout << matrix[i * n + j] << "\t";
    }
    cout << endl;
  }
}

// Обмен строк в матрице
void swap_lines(double *matrix, double *identity, int n, int i, int j) {
  double temp;
  for (int k = 0; k < n; k++) {
    temp = matrix[i * n + k];
    matrix[i * n + k] = matrix[j * n + k];
    matrix[j * n + k] = temp;

    temp = identity[i * n + k];
    identity[i * n + k] = identity[j * n + k];
    identity[j * n + k] = temp;
  }
}

// Поставить на место row строку с наибольшим ведущим коэффициентом
void pivotize(double *matrix, double *identity, int n, int row) {
  int max_index = row;
  double max_value = fabs(matrix[row * n + row]);
  double current_value;
  for (int i = row + 1; i < n; i++) {
    current_value = fabs(matrix[i * n + row]);
    if (current_value > max_value) {
      max_index = i;
      max_value = current_value;
    }
  }

  if (row != max_index) {
    swap_lines(matrix, identity, n, row, max_index);
  }
}

// Разделить строку матрицы на значение
void devide(double *matrix, int n, int i, double denominator) {
  for (int j = 0; j < n; j++) {
    matrix[i * n + j] /= denominator;
  }
}

// Обнуление элементов под ведущим элементом в строке x
void subtract_below(double *matrix, double *identity, int n, int x) {
  double coeff;
  for (int i = x + 1; i < n; i++) {
    coeff = matrix[i * n + x] / matrix[x * n + x];
    for (int j = x; j < n; j++) {
      matrix[i * n + j] -= coeff * matrix[x * n + j];
    }
    for (int j = 0; j < n; j++) {
      identity[i * n + j] -= coeff * identity[x * n + j];
    }
  }
}

// Обнуление элементов над ведущим элементом в строке x
void subtract_above(double *matrix, double *identity, int n, int x) {
  double coeff;
  for (int i = x - 1; i >= 0; i--) {
    coeff = matrix[i * n + x] / matrix[x * n + x];
    for (int j = x; j >= 0; j--) {
      matrix[i * n + j] -= coeff * matrix[x * n + j];
    }
    for (int j = 0; j < n; j++) {
      identity[i * n + j] -= coeff * identity[x * n + j];
    }
  }
}

// Обращение матрицы методом Гаусса-Жордана
void inverse(double *matrix, double *identity, int n) {
  // Прямой ход
  for (int i = 0; i < n - 1; i++) {
    // Обмен строк
    pivotize(matrix, identity, n, i);

    // Обнулить элементы ниже ведущего
    subtract_below(matrix, identity, n, i);
  }

  // Обратный ход
  for (int i = n - 1; i > 0; i--) {
    // Обнулить элементы выше ведущего
    subtract_above(matrix, identity, n, i);
  }

  // Разделить строки на ведущие элементы
  for (int i = 0; i < n; i++) {
    devide(identity, n, i, matrix[i * n + i]);
    devide(matrix, n, i, matrix[i * n + i]);
  }
}

int main() {
  int n;
  cin >> n;

  double *matrix = new double[n * n];
  double *identity = new double[n * n];

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      cin >> matrix[i * n + j];
    }
  }

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      identity[i * n + j] = i == j ? 1.0 : 0.0;
    }
  }

  inverse(matrix, identity, n);
  print(identity, n);

  delete[] matrix;
  delete[] identity;

  return 0;
}

Что нужно для написания версии под CUDA?

• Выделить независимые подпрограммы, которые можно распараллелить:
  1. pivotize — поиск масимального ведущего элемента и обмен строк,
  2. subtract_below — обнуление элементов ниже ведущего,
  3. subtract_above — обнуление элементов выше ведущего (обратный ход),
  4. devide — деление строк на их ведущие элементы.
• Привести подпрограммы к выполнению однотипных действий:
  1. функция pivotize разделена на две:
     • max_in_column — поиск максимального ведущего элемента (индекс max_element_index сохраняется в глобальную память GPU)
     • swap_lines — обмен строк (обмен текущей строки со строкой с индексом max_element_index)
  2. функция subtract_below разделена на:
     • subtract_below — вычитание текущей строки из нижележащих строк правее ведущего столбца с целью обнулить элементы ниже ведущего
     • nullify_below — обнуление элементов в столбце под ведущим
  3. функция subtract_above разделена на:
     • subtract_above — вычитание текущей строки из вышележащих строк левее ведущего столбца с целью обнулить элементы выше ведущего
     • nullify_above — обнуление элементов в столбце над ведущим
  4. функция devide разделена на:
     • devide_identity — разделить строки правой матрицы на диагональные элементы левой матрицы
     • devide_matrix — заменить все диагональные элементы в левой матрице на единицы

Итоговый код на CUDA:

#include <iostream>
#include <cmath>

#define DEBUG false
#define DEBUG_MATRIX false
#define DEBUG_TIMER true

using namespace std;

// Индекс строки с максимальным элементом из find_max_element_in_columnt()
__device__ int max_element_index;

void print(double* matrix, int n) {
  cout << scientific;
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      cout << matrix[i * n + j] << "\t";
    }
    cout << endl;
  }
}

void print_both(double* matrix, double* identity, int n) {
  cout << scientific;
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < 2 * n; j++) {
      if (j < n) {
        cout << matrix[i * n + j] << "\t";
      } else {
        cout << identity[i * n + j - n] << "\t";
      }
    }
    cout << endl;
  }
}

// Обмен строк
__global__ void swap_lines(double* matrix, double* identity, int n, int row) {
  if (row == max_element_index) {
    return;
  }

  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  int offset = gridDim.x * blockDim.x;

  double temp;
  for (; idx < n; idx += offset) {
    temp = matrix[row * n + idx];
    matrix[row * n + idx] = matrix[max_element_index * n + idx];
    matrix[max_element_index * n + idx] = temp;

    temp = identity[row * n + idx];
    identity[row * n + idx] = identity[max_element_index * n + idx];
    identity[max_element_index * n + idx] = temp;
  }
}

// Сохранение индекса строки с максимальным элементом в max_element_index на GPU
__global__ void max_in_column(double* matrix, int n, int x) {
  int max_index = x;
  double max_value = fabs(matrix[x * n + x]);
  double current_value;

  for (int i = x + 1; i < n; i++) {
    current_value = fabs(matrix[i * n + x]);
    if (current_value > max_value) {
      max_index = i;
      max_value = current_value;
    }
  }

  max_element_index = max_index;
}

__global__ void devide_identity(double* matrix, double* identity, int n) {
  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  int idy = blockIdx.y * blockDim.y + threadIdx.y;
  int offsetx = gridDim.x * blockDim.x;
  int offsety = gridDim.y * blockDim.y;

  for (int i = idx; i < n; i += offsetx) {
    for (int j = idy; j < n; j += offsety) {
      identity[i * n + j] /= matrix[i * n + i];
    }
  }
}

__global__ void devide_matrix(double* matrix, int n) {
  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  int offsetx = gridDim.x * blockDim.x;
  for (int i = idx; i < n; i += offsetx) {
    matrix[i * n + i] = 1.0;
  }
}

// Обнуление элементов под ведущим элементом в строке x
__global__ void subtract_below(double* matrix, double* identity, int n, int x) {
  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  int idy = blockIdx.y * blockDim.y + threadIdx.y;
  int offsetx = gridDim.x * blockDim.x;
  int offsety = gridDim.y * blockDim.y;

  int i, j;
  double coeff;
  for (i = x + 1 + idx; i < n; i += offsetx) {
    coeff = matrix[i * n + x] / matrix[x * n + x];
    for (j = x + 1 + idy; j < n; j += offsety) {
      matrix[i * n + j] -= coeff * matrix[x * n + j];
    }
    for (j = idy; j < n; j += offsety) {
      identity[i * n + j] -= coeff * identity[x * n + j];
    }
  }
}

__global__ void nullify_below(double* matrix, int n, int x) {
  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  int offsetx = gridDim.x * blockDim.x;
  for (int i = x + 1 + idx; i < n; i += offsetx) {
    matrix[i * n + x] = 0.0;
  }
}

// Обнуление элементов над ведущим элементом в строке x
__global__ void subtract_above(double* matrix, double* identity, int n, int x) {
  int idx = threadIdx.x + blockIdx.x * blockDim.x;
  int idy = threadIdx.y + blockIdx.y * blockDim.y;
  int offsetx = gridDim.x * blockDim.x;
  int offsety = gridDim.y * blockDim.y;

  int i, j;
  double coeff;
  for (i = x - 1 - idx; i >= 0; i -= offsetx) {
    coeff = matrix[i * n + x] / matrix[x * n + x];
    for (j = x - 1 - idy; j >= 0; j -= offsety) {
      matrix[i * n + j] -= coeff * matrix[x * n + j];
    }
    for (j = idy; j < n; j += offsety) {
      identity[i * n + j] -= coeff * identity[x * n + j];
    }
  }
}

__global__ void nullify_above(double* matrix, int n, int x) {
  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  int offsetx = gridDim.x * blockDim.x;
  for (int i = x - idx - 1; i >= 0; i -= offsetx) {
    matrix[i * n + x] = 0.0;
  }
}

// Обращение матрицы методом Гаусса-Жордана
void inverse_gpu(double* matrix, double* identity, int n) {
  dim3 BLOCKS_1D(16);
  dim3 THREADS_1D(32);
  dim3 BLOCKS_2D(16, 16);
  dim3 THREADS_2D(32, 32);

  double* dev_matrix;
  double* dev_identity;
  cudaMalloc(&dev_matrix, sizeof(double) * n * n);
  cudaMalloc(&dev_identity, sizeof(double) * n * n);
  cudaMemcpy(dev_matrix, matrix, sizeof(double) * n * n,
             cudaMemcpyHostToDevice);
  cudaMemcpy(dev_identity, identity, sizeof(double) * n * n,
             cudaMemcpyHostToDevice);

  cudaEvent_t start, stop;

  if (DEBUG && DEBUG_TIMER) {
    cudaEventCreate(&start);
    cudaEventCreate(&stop);
    cudaEventRecord(start, 0);
  }

  // Прямой ход
  for (int i = 0; i < n; i++) {
    // Обменять строку со строкой с наибольшим ведущим элементом и обнулить
    // элементы под ним
    max_in_column<<<1, 1>>>(dev_matrix, n, i);
    swap_lines<<<BLOCKS_1D, THREADS_1D>>>(dev_matrix, dev_identity, n, i);
    subtract_below<<<BLOCKS_2D, THREADS_2D>>>(dev_matrix, dev_identity, n, i);
    nullify_below<<<BLOCKS_1D, THREADS_1D>>>(dev_matrix, n, i);
  }

  // Обратный ход
  for (int i = n - 1; i >= 0; i--) {
    // Обнулить элементы выше ведущего
    subtract_above<<<BLOCKS_2D, THREADS_2D>>>(dev_matrix, dev_identity, n, i);
    nullify_above<<<BLOCKS_1D, THREADS_1D>>>(dev_matrix, n, i);
  }

  // Разделить строки на их ведущие элементы
  devide_identity<<<BLOCKS_2D, THREADS_2D>>>(dev_matrix, dev_identity, n);
  devide_matrix<<<BLOCKS_1D, THREADS_1D>>>(dev_matrix, n);

  if (DEBUG && DEBUG_TIMER) {
    cudaGetLastError();
    cudaEventRecord(stop, 0);
    cudaEventSynchronize(stop);
    float t;
    cudaEventElapsedTime(&t, start, stop);
    cout << t << endl;
    cudaEventDestroy(start);
    cudaEventDestroy(stop);
  }

  cudaMemcpy(matrix, dev_matrix, sizeof(double) * n * n,
             cudaMemcpyDeviceToHost);
  cudaMemcpy(identity, dev_identity, sizeof(double) * n * n,
             cudaMemcpyDeviceToHost);
  cudaFree(dev_matrix);
  cudaFree(dev_identity);
}

int main() {
  int n;
  cin >> n;

  double* matrix = new double[n * n];
  double* identity = new double[n * n];

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      cin >> matrix[i * n + j];
    }
  }

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      identity[i * n + j] = i == j ? 1.0 : 0.0;
    }
  }

  if (DEBUG && DEBUG_MATRIX) {
    cout << "Before:" << endl;
    print_both(matrix, identity, n);
    cout << endl;
  }

  inverse_gpu(matrix, identity, n);

  if (DEBUG && DEBUG_MATRIX) {
    cout << "After:" << endl;
    print_both(matrix, identity, n);
    cout << endl;
  }

  if (!DEBUG) {
    // Вывести обратную матрицу
    print(identity, n);
  }

  delete[] matrix;
  delete[] identity;

  return 0;
}

Заключение

Подход к параллельным вычислениям предлагаемый Nvidia довольно прост: ускорить циклы с однотипными действиями.

Стоит отметить, что основная сложность при написании программ на CUDA — выделение тех частей алгоритма, которые можно распараллелить.

Было бы очень интересно найти применение CUDA в реальном проекте.

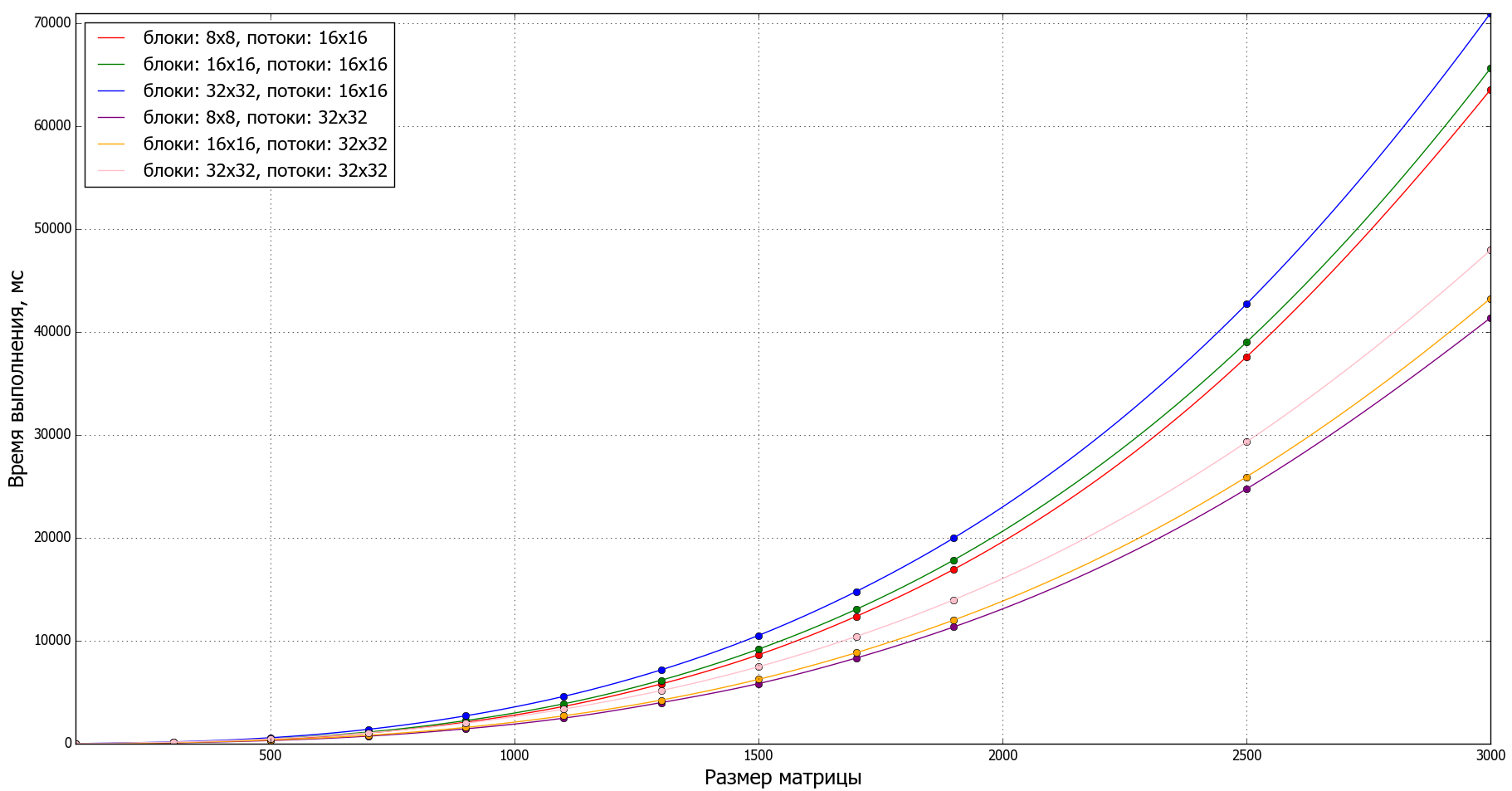
Графики

Для анализа производительности программы с помощью Python и matplotlib были построены графики для разных вычислительных сеток.

import os
from os.path import basename, splitext
from numpy import linspace, array
import matplotlib
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from multiprocessing import Pool

# Настройка шрифтов
matplotlib.rc('font', family='Tahoma', size=16)
matplotlib.rc('axes', titlesize=22)
matplotlib.rc('axes', labelsize=18)
matplotlib.rc('legend', fontsize=16)
matplotlib.rc('xtick', labelsize=12)
matplotlib.rc('ytick', labelsize=12)


# Время выполнения для теста <size> для программы <program_name>
def calculate_time(params):
    program_name = params['program_name']
    size = params['size']
    testname = 'test{}.txt'.format(size)
    if not os.path.isfile(testname):
        return None
    output = os.popen('{} < {}'.format(program_name, testname)).read()
    output = float(output)
    print('Программа {}, тест {}, время {} мс'.format(program_name, testname, output))
    return {'size': size, 'time': output}


# Расчёт времени выполнения для сеток от 1x1 до 2000x2000 для существующих тестов
def run_test_for_program(program_name):

    params = [{'program_name': program_name, 'size': n} for n in range(3000 + 1)]
    result = Pool(4).map(calculate_time, params)
    result = [x for x in result if x is not None]
    x = array([float(x['size']) for x in result])
    y = array([x['time'] for x in result])
    return x, y


# Данные измерений
def get_functions():
    return [
        {
            'label': 'блоки: 8x8, потоки: 16x16',
            'color': 'red',
            'data': run_test_for_program('lab1_8x8_16x16.exe')
        },
        {
            'label': 'блоки: 16x16, потоки: 16x16',
            'color': 'green',
            'data': run_test_for_program('lab1_16x16_16x16.exe')
        },
        {
            'label': 'блоки: 32x32, потоки: 16x16',
            'color': 'blue',
            'data': run_test_for_program('lab1_32x32_16x16.exe')
        },
        {
            'label': 'блоки: 8x8, потоки: 32x32',
            'color': 'purple',
            'data': run_test_for_program('lab1_8x8_32x32.exe')
        },
        {
            'label': 'блоки: 16x16, потоки: 32x32',
            'color': 'orange',
            'data': run_test_for_program('lab1_16x16_32x32.exe')
        },
        {
            'label': 'блоки: 32x32, потоки: 32x32',
            'color': 'pink',
            'data': run_test_for_program('lab1_32x32_32x32.exe')
        }
    ]


# Функция апроксимации
def fit_quadratic_function(x, a, b, c):
    return a * x ** 2 + b * x + c


def main():
    plt.figure(figsize=(22, 11), dpi=80)

    x_min, x_max = None, None
    y_min, y_max = None, None

    for f in get_functions():
        label = f['label']
        color = f['color']
        x, y = f['data']

        if not all([x_min, x_max, y_min, y_max]):
            x_min, x_max = x.min(), x.max()
            y_min, y_max = y.min(), y.max()
        else:
            x_min, x_max = min(x_min, x.min()), max(x_max, x.max())
            y_min, y_max = min(y_min, y.min()), max(y_max, y.max())

        x_new = linspace(x.min(), x.max(), 100)
        f = interp1d(x, y, kind='cubic')
        plt.plot(x, y, marker='o', linestyle='', color=color)
        plt.plot(x_new, f(x_new), linestyle='-', color=color, label=label)

    # Внешний вид
    plt.xlim([x_min, x_max])
    plt.ylim([y_min, y_max])
    plt.xlabel('Размер матрицы')
    plt.ylabel('Время выполнения, мс')
    plt.legend(loc='best')
    plt.grid(True)

    # Сохранить в PNG и показать
    file_name, file_extension = splitext(__file__)
    plt.savefig('{:s}.png'.format(basename(file_name)))
    plt.show()


if __name__ == "__main__":
    main()

Расчёты были проведены на сетках размеров от 100x100 до 3000x3000.

Графики производительности для разных сеток: